Computing the Bounding Box of a Coordinate Grid of Soil Moisture Data

Today I learned about coordinate grids and how to calculate the bounding box of a grid when you have the centers of the pixels in the grid. So for more context, I was reviewing a PR for a refactor of our soil moisture acquisition logic when i encountered a strange formula:

ymin = y0 - ywidth/2
xmin = x0 - xwidth/2
ymax = yN + ywidth/2
xmax = xN + xwidth/2

where xwidth and ywidth are pixel widths.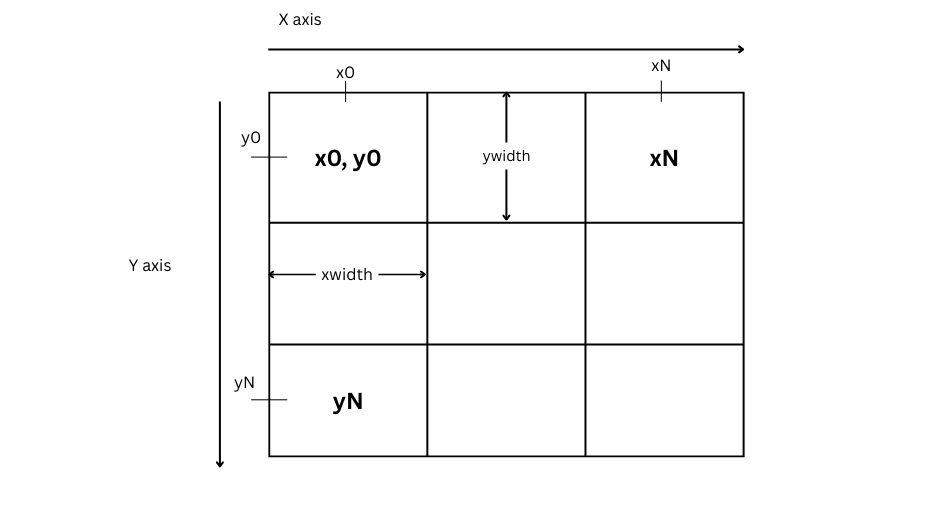

This formula was used to calculate the bounding box of the soil moisture grid returned by the API. We usually can’t use the grid as is because we require rasters for our use cases, so we had to compute the bounding box of the grid to derive the raster extent.

How the formula works

Now, in this formula, you are given the center of a given pixel in a grid and you want to figure out the bottom left, bottom right, top right, and top left coordinates. In other words, xmin, xmax, ymin and ymax. In our case the pixels in the grid were of equal width, so calculating the width of a pixel was as easy as subtracting the center of the first pixel from the center of the pixel after it.

xwidth = x2-x1
ywidth = y2-y1

Now that we have the width, we can easily calculate xmin, xmax, ymin and ymax.

To get xmin, we simply move xwidth/2 left (subtract) from x0, likewise for ymin, simply move ywidth/2 from y0. It’s the same for xmax and ymax, but since we’re moving toward the right now, we’ll be adding, so that will be xmax plus the xwidth/2 and similar for ymax.

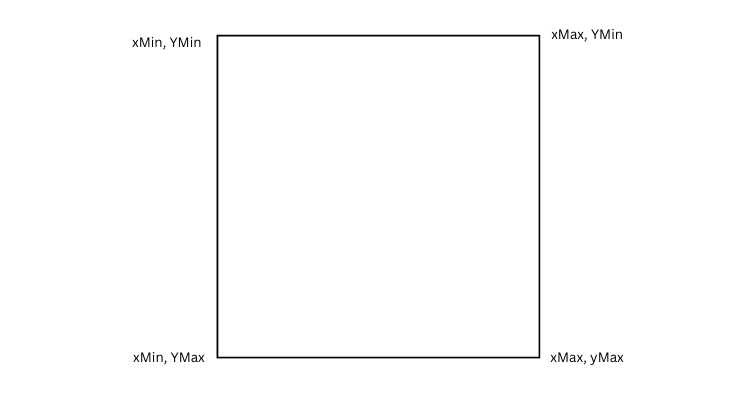
And that’s it. The bounding box is defined by the coordinates xMin, Ymin, xMax, YMin, XMin, YMax, XMax, YMax.

Conclusion

It’s always a joy to gain more knowledge about the domain you work in. Until now I’d been aware of the concept of a bounding box but never stopped to think about how to actually derive one. Discovering this formula has given me—insignificant but nevertheless important—insight into the mechanics of GIS and geometry. That’s a good thing.

You live, you learn.

Onward to mastery.